Glossary¶

Piecewise Polynomial¶

A piecewise function is function of the form

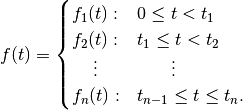
$f(t) = \begin{cases} f_1(t) :& 0 \leq t < t_1 \\ f_2(t) :& t_1 \leq t < t_2 \\ \hfill \vdots \hfill & \hfill \vdots \hfill \hfill \\ f_n(t) :& t_{n - 1} \leq t \leq t_n. \end{cases}$

where 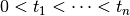$0 < t_1 < \cdots < t_n$ . It is naturally possible to define piecewise functions on unbounded domains too, but in typical applications the domain is bounded.

A piecewise polynomial is a piecewise function where each of the $f_i(t)$ is a polynomial, possibly vector-valued. With suitable number of pieces and polynomial degree, piecewise polynomials make a highly expressive function class that is still simple and numerically stable.

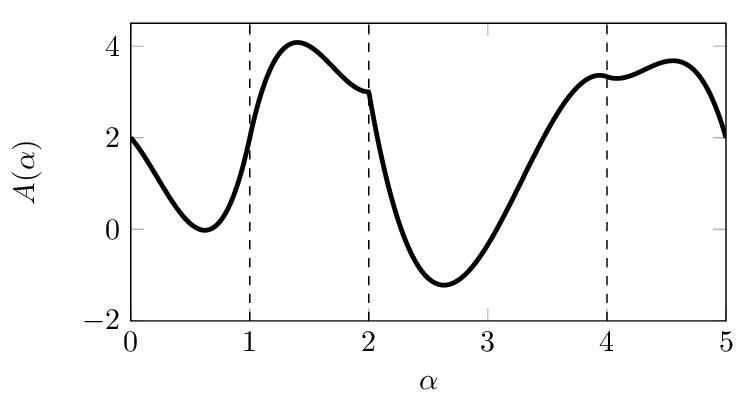
_images/piecewise_poly.png — A piecewise polynomial with four pieces. At the point 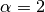$\alpha = 2$ , this function is continuous but not differentiable. Such a nonsmooth polynomial would not be used for quadrotor trajectory planning.¶

A piecewise polynomial with four pieces. At the point $\alpha = 2$ , this function is continuous but not differentiable. Such a nonsmooth polynomial would not be used for quadrotor trajectory planning.¶

In Crazyswarm, we use degree-7 polynomials with 4-dimensional vector-valued output: (x, y, z) position and yaw angle. The quadrotor’s differential flatness property makes it possible to compute other states (attitude, acceleration, angular velocity) from these four values.

Setpoint¶

A collection of desired values for some or all of the quadrotor’s state that the feedback controller should try to achieve. For example, a setpoint may specify position, velocity, and acceleration – or just position.